Soal 1 : Balok Sederhana dengan Kantilever di Sisi Kanan
Hitung
dan gambar bidang M, L, N dari struktur di atas.
Pada
soal ini, arah reaksi perletakan diasumsi sebagai berikut :
VA
ke atas (↑)
VB
ke atas (↑)
HA
ke kanan (→)
Σ
H = 0 → HA - 400 + 200 = 0
HA = 200 kN (→)
Σ
MA = 0 → -VB (5) + (600 x 3) (1.5) + 400(3) + 200(7) = 0
5VB
= 5300
VB = 1060 kN (↑)
Σ
MB = 0 → VA (5) + 200 (2) - 400 (2) - (600 x 3)(3.5) = 0
5VA
= 6700
VA = 1340 kN (↑)
Check
Σ V = 0?
VA
+ VB - (600x3) - 400 - 200 = 0
1340
+ 1060 - 1800 - 600 = 0 (OK)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Interval 1 (0 < x1
< 3m) [lihat
kiri]
Mx1
= +VA x1 - q
x1 (0.5 x1)
= 1340 x1 - 0.5 (600)
(x12)
= 1340 x1 - 300x12
(persamaan derajat 2 / pangkat 2)
x1
= 0 → Mx1 = 0
x1
= 1.5 m → Mx1 = 1335 kNm (∪)
x1
= 3 m → Mx1 = 1320 kNm (∪)
Lx1
= +VA - q x1
= 1340 - 600 x1
x1
= 0 → Lx1 = 1340 kN (↿⇂)
x1
= 3 m → Lx1 = -460 kN (⇃↾)
Mencari
letak dan besaran momen maksimum : Lx
= 0
1340
- 600 x1 = 0 → x1 = 2.2333 m
Mmax
= 1340 (2.2333) - 300 (2.2333)2 = 1496.3333 kNm
Nx1
= -HA = -200 kN (tekan)
Interval 2 (0 < x2
< 2m) [lihat
kanan]
Mx2
=
-200x2 (garis lurus / linear)
x2
= 0 → Mx2 = 0
x2
= 2 m → Mx2 = -400 kNm (∩)
Lx2
= 200 kN (↿⇂)
Nx2
= 2000 kN (tarik)
Interval 3 (0 < x3
< 2 m) [lihat
kiri]
Mx3
=
-200(2 + x3) + VB x3
= 860 x3 - 400 (garis lurus / linear)
x3
= 0 → Mx3 = -400 kNm (∩)
x3
= 2 m → Mx2 = 1720 - 400 =
1320 kNm (∪)
Lx3
= 200 - VB = 200 - 1060 = -860 kN (⇃↾)
Nx3
= 200 kN (tarik)
Hasil
perhitungan nilai gaya dalam di atas kemudian diplot untuk mendapatkan bidang gaya dalam.
Gambar Bidang Gaya Dalam (M, L, N)
*bidang gaya dalam tidak berskala
Urutan gambar dari atas ke bawah adalah, bidang momen lentur, bidang gaya lintang, bidang gaya normal.
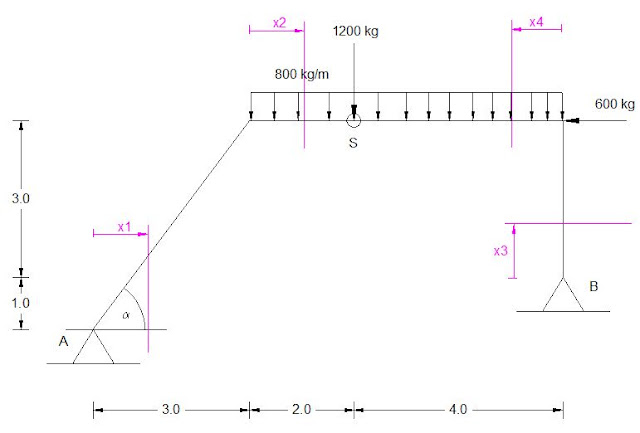
Soal 2 : Portal Sederhana dengan Kantilever
Hitung
dan gambar bidang M, L, N
tanα
= 4/3 sinα = 0.8 cosα = 0.6
Pada
soal ini, arah reaksi perletakan diasumsi sebagai berikut :
VA
ke atas (↑)
VB
ke atas (↑)
HA
ke kanan (→)
Σ
H = 0 → HA + 30 = 0
HA
= -30 kN (asumsi salah)
HA
= 30 kN (→)
Σ
MA = 0 → -VB (8) + 30(10) + 30(4) + (40 x 5)(3+2.5) +
60(1.5) =0
VB
= 201.25 kN (↑)
Σ
MB = 0 → VA (8) + HA (4) - 60 (1.5 +5) - (40 x
5)2.5 + 30(2) = 0
8VA
= 710
VA
= 88.75 kN (↑)
Check
Σ V = 0?
VA
+ VB - 60 - (40 x 5) - 30 = 0
88.75
+ 201.25 - 60 -200 -30 = 0 (OK)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Interval 1 (0 < x1
< 1.5 m)
Mx1
= VA (x1) + HA
tan α x1
= 88.75 x1 +
40x1 = 128.75x1
x1
= 0 → Mx1 = 0
x1
= 1.5 m → Mx1 = 193.125 kN m (∪)
Lx1
= VA cos α + HA
sin α
= 88.75 (0.6) + 30 (0.8) = 77.25
kN (↿⇂)
Nx1
= -VA sin α + HA
cos α
= -88.75 (0.8) + 30 (0.6) = -53 kN
(tekan)
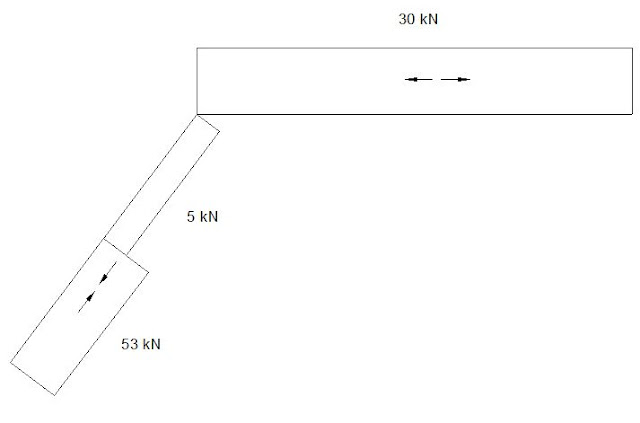
Interval 2 (0 < x2 < 1.5 m)
Mx2
= VA (1.5 + x2)
+ HA (2 + 4/3 x2) - 60 x2
= 193.125 + 68.75 x2
x2
= 0 → Mx2 = 193.125 kNm (∪)
x2
= 1.5 m → Mx2 = 296.25 kNm (∪)
Lx2
= VA cos α + HA
sin α - 60 cos α
= 88.75 (0.6) + 30 (0.8) - 60
(0.6) = 41.25 kN (↿⇂)
Nx2
= -VA sin α + HA
cos α + 60 sin α
= -88.75 (0.8) + 30 (0.6) + 60
(0.8) = -5 kN (tekan)
Interval 3 (0 < x3
< 2m)
Mx3 = - 30 x3
x3
= 0 → Mx3 = 0
x3
= 2 m → Mx3 = -60 kNm (∩)
Lx3
= 30 kN (↿⇂)
Nx3
= 30 kN (tarik)
Interval 4 (0 < x4
< 5m)
Mx4
= - 30 (2 + x4) - q x4
(0.5 x4) + VB (x4)
= -20 x42 +
171.25 x4 - 60
x4
= 0 → Mx4 = 0
x4
= 2.5 m → Mx4 = 243.125 kNm (∪)
x4
= 5 m → Mx4 = 296.25 kNm (∪)
Mencari
letak dan besaran momen maksimum : Lx
= 0
-40
x4 + 171.25 = 0 → x4 = 4.28125 m
Mmax
= -20 (4.28125) 2 + 171.25 (4.28125)
- 60= 306.5820 kNm
Lx4
= 30 - VB + q x4
= 171.25 + 40x4
x4
= 0 → Lx4 = -171.25 kN (⇃↾)
x4
= 5 m → Lx4 = 28.75 kN (↿⇂)
Nx4
= 30 kN (tarik)
Gambar Bidang Gaya Dalam (M, L, N) *tidak berskala
Bidang Momen Lentur
Bidang Gaya Lintang
Bidang Gaya Normal
Soal 3: Balok Kantilever
Hitung dan gambar bidang M, L, N
Σ V = 0 → VA - (40 x 3) - 60 = 0
VA = 180 kN (↑)
Σ H = 0 → -HA + 60 = 0
HA = 60 kN (←)
Σ MA = 0 → -MA + 120(1.5) + 60(6)
= 0
MA = 540 kN m (↺)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Interval 1 (0 < x1
< 3m)
Mx1 =
-MA + VA x1 - q x1 (0.5 x1)
=
-20 x12 + 180 x1 - 540
x1 = 0 → Mx1 = -540 kN m (∩)
x1 = 1.5 m → Mx1 = -315 kN m (∩)
x1 = 3 m → Mx1 = -180 kN m (∩)
Lx1 = VA - 40x1 = 180
- 40x1
x1 = 0 → Lx1 = 180 kN (↿⇂)
x1 = 3 m → Lx1 = 60 kN (↿⇂)
Nx1 = HA = 60 kN (tarik)
Interval 2 (0 < x2
< 3m)
Mx2 = -60x2
x2 = 0 → Mx2 = 0
x2 = 3 m → Mx2 = -180 kN m (∩)
Lx2 = 80 kN (↿⇂)
Nx2 = 60 kN (tarik)
Gambar Bidang Gaya Dalam (M, L, N) *tidak berskala
Soal 4: Portal Jepit Bebas
Hitung dan gambar bidang gaya dalam
tan
α = 1.5 / 3 = 0.5
α
= 26.5651°
tan
β = 1.5 / 4 = 0.275
β
= 20.5560°
Σ
V = 0 → VA - 160 - 20 = 0
VA
= 180 kN (↑)
Σ
H = 0 → -30 + HA = 0
HA
= 30 kN (→)
Σ
MA = 0 → 160 (2) - 30(6 + 1.5) - 20(3) - MA = 0
MA
= 35 kN m (↺)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Interval 1 (0 < x1
< 6 m)
Mx1
= -MA - HA x1 = -35 - 30x1
x1
= 0 → Mx1 = -35 kNm (∩)
x1
= 6 m → Mx1 =-215 kNm (∩)
Lx1
= -HA = -30 kN (⇃↾)
Nx1
= -VA = -180 kN (tekan)
Interval 2 (0 < x2
< 3 m)
Mx2
= -20x2
x2
= 0 → Mx2 = 0
x2
= 3 m → Mx2 = -60 kNm (∩)
Lx2
= -P cos α = -20 cos (26.5651° ) = -17.8892 kN
(⇃↾)
Nx2
= -P sin α = -20 sin (26.5651°) = - 8.9443 kN (tekan)
Interval 3 (0 < x3
< 4 m)
Mx3
= -q x3 (0.5 x3)
+ 30 tan β x3
= -20x32 +
11.25 x3
x3
= 0 → Mx3 = 0
x3
= 2 m → Mx3 = -57.5 kN m
x3
= 4 m → Mx3 = -275 kN m
Letak
dan besar momen maksimum :
x3 = 0.2812 m
Mmax = -20(0.2812) 2 + 11.25
(0.2812) = 1.582 kN m (∪)
Lx3 =
q x3 cos β - 30 sin β
=
37.4532 x3 - 10.5337
x3 = 0 → Lx3 = -10.5337 kN (⇃↾)
x3 = 4 m → Lx3 = 139.2591 kN (↿⇂)
Nx3 =
-q x3 sin β - 30 cos β
=
-14.0449 x3 - 28.0899
x3 = 0 → Nx3 = -28.0899kN (tekan)
x3 = 4 m → Nx3 = -84.2695 kN (tekan)
Check keseimbangan momen titik B
Σ MB = 0 → 215 +60 - 275 = 0 (OK)
Bidang Momen Lentur
Bidang Gaya Lintang

Bidang Gaya Normal
Soal 5 : Portal dengan beban lateral / horisontal
Hitung
dan gambar bidang M, L, N
Pada
soal ini, arah reaksi perletakan diasumsi sebagai berikut :
VA
ke atas (↑)
VB
ke atas (↑)
HB
ke kanan (→)
tan
α = 4/3 sin α = 0.8 cos α = 0.6
Σ
H = 0 → HB - 1200 + (800 x 4) = -2000 kg (asumsi salah)
HB
= 2000 kg (←)
Σ MA = 0 → (800 x 4) (2) - 1200 (4) - VB
(4) = 0
4 VB = 1600
VB = 400 kg (↑)
Σ MB = 0 → (800 x 4) (2) - 1200 (4) + VA
(4) = 0
4 VA
= -1600
VA = -400 (pemisalan salah)
VA = 400 kg (↓)
Interval untuk menghitung gaya dalam ditentukan sebagai
berikut :
Mx1
= -0.5 q x12 = -40 x12
x1
= 2 m → Mx1 = -1600 kg m (∩)
x1
= 4 m → Mx1 = -6400 kg m (∩)
x1
= 4m → Lx1 = - 3200 kg (⇃↾)
Nx1
= VA = 400 kg (tarik)
Interval
2 (0 < x2 < 7 m)
Mx2
= -VA x2 - (800 x 4)2 = -400 x2 - 6400
x2
= 0 → Mx2 = -6400 kg m
x2
= 7 m → Mx2 = -9200 kg m
Lx2
= -VA = - 400 kg (⇃↾)
Nx2
= - (800 x 4) = -3200 kg (tekan)
Interval
3 (0 < x3 < 3 m)
Mx3
= -VB x3 - HB (4/3 x3) = -3066.667
x3
x3
= 3 m → Mx3 = -9200 kg m
Lx3
= VB cos α + HB sin α
= 400 (0.6) + 2000 (0.8) = 1840 kg (↿⇂)
Nx3
= -VB sin α + HB cos α = -400 (0.8) + 2000 (0.6) = 880 kg
(tarik)
Bidang
Gaya Dalam (*tidak berskala)
Bidang Momen Lentur
Bidang Gaya Lintang
Bidang Gaya Normal