Soal 1 : Balok Sederhana dengan Kantilever di Sisi Kanan
Pada
soal ini, arah reaksi perletakan diasumsi sebagai berikut :
VA
ke atas (↑)
VB
ke atas (↑)
HA
ke kanan (→)
Σ
H = 0 → HA - 400 + 200 = 0
HA = 200 kN (→)
Σ
MA = 0 → -VB (5) + (600 x 3) (1.5) + 400(3) + 200(7) = 0
5VB
= 5300
VB = 1060 kN (↑)
Σ
MB = 0 → VA (5) + 200 (2) - 400 (2) - (600 x 3)(3.5) = 0
5VA
= 6700
VA = 1340 kN (↑)
Check
Σ V = 0?
VA
+ VB - (600x3) - 400 - 200 = 0
1340
+ 1060 - 1800 - 600 = 0 (OK)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Mx1
= +VA x1 - q
x1 (0.5 x1)
= 1340 x1 - 0.5 (600)
(x12)
= 1340 x1 - 300x12
(persamaan derajat 2 / pangkat 2)
x1
= 0 → Mx1 = 0
x1
= 1.5 m → Mx1 = 1335 kNm (∪)
x1
= 3 m → Mx1 = 1320 kNm (∪)
Lx1
= +VA - q x1
= 1340 - 600 x1
x1
= 0 → Lx1 = 1340 kN (↿⇂)
x1
= 3 m → Lx1 = -460 kN (⇃↾)
Mencari
letak dan besaran momen maksimum : Lx
= 0
1340
- 600 x1 = 0 → x1 = 2.2333 m
Mmax
= 1340 (2.2333) - 300 (2.2333)2 = 1496.3333 kNm
Nx1
= -HA = -200 kN (tekan)
Interval 2 (0 < x2
< 2m) [lihat
kanan]
Mx2
=
-200x2 (garis lurus / linear)
x2
= 0 → Mx2 = 0
x2
= 2 m → Mx2 = -400 kNm (∩)
Lx2
= 200 kN (↿⇂)
Nx2
= 2000 kN (tarik)
Interval 3 (0 < x3
< 2 m) [lihat
kiri]
Mx3
=
-200(2 + x3) + VB x3
= 860 x3 - 400 (garis lurus / linear)
x3
= 0 → Mx3 = -400 kNm (∩)
x3
= 2 m → Mx2 = 1720 - 400 =
1320 kNm (∪)
Lx3
= 200 - VB = 200 - 1060 = -860 kN (⇃↾)
Nx3
= 200 kN (tarik)
Hasil
perhitungan nilai gaya dalam di atas kemudian diplot untuk mendapatkan bidang gaya dalam.
Gambar Bidang Gaya Dalam (M, L, N)
Urutan gambar dari atas ke bawah adalah, bidang momen lentur, bidang gaya lintang, bidang gaya normal.
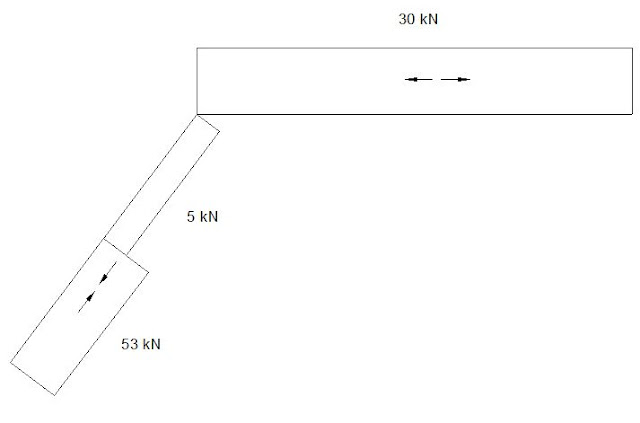
Soal 2 : Portal Sederhana dengan Kantilever
Hitung
dan gambar bidang M, L, N
tanα
= 4/3 sinα = 0.8 cosα = 0.6
Pada
soal ini, arah reaksi perletakan diasumsi sebagai berikut :
VA
ke atas (↑)
VB
ke atas (↑)
HA
ke kanan (→)
Σ
H = 0 → HA + 30 = 0
HA
= -30 kN (asumsi salah)
HA
= 30 kN (→)
Σ
MA = 0 → -VB (8) + 30(10) + 30(4) + (40 x 5)(3+2.5) +
60(1.5) =0
VB
= 201.25 kN (↑)
Σ
MB = 0 → VA (8) + HA (4) - 60 (1.5 +5) - (40 x
5)2.5 + 30(2) = 0
8VA
= 710
VA
= 88.75 kN (↑)
Check
Σ V = 0?
VA
+ VB - 60 - (40 x 5) - 30 = 0
88.75
+ 201.25 - 60 -200 -30 = 0 (OK)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Interval 1 (0 < x1
< 1.5 m)
Mx1
= VA (x1) + HA
tan α x1
= 88.75 x1 +
40x1 = 128.75x1
x1
= 0 → Mx1 = 0
x1
= 1.5 m → Mx1 = 193.125 kN m (∪)
Lx1
= VA cos α + HA
sin α
= 88.75 (0.6) + 30 (0.8) = 77.25
kN (↿⇂)
Nx1
= -VA sin α + HA
cos α
= -88.75 (0.8) + 30 (0.6) = -53 kN
(tekan)
Interval 2 (0 < x2 < 1.5 m)
Mx2
= VA (1.5 + x2)
+ HA (2 + 4/3 x2) - 60 x2
= 193.125 + 68.75 x2
x2
= 0 → Mx2 = 193.125 kNm (∪)
x2
= 1.5 m → Mx2 = 296.25 kNm (∪)
Lx2
= VA cos α + HA
sin α - 60 cos α
= 88.75 (0.6) + 30 (0.8) - 60
(0.6) = 41.25 kN (↿⇂)
Nx2
= -VA sin α + HA
cos α + 60 sin α
= -88.75 (0.8) + 30 (0.6) + 60
(0.8) = -5 kN (tekan)
Interval 3 (0 < x3
< 2m)
Mx3 = - 30 x3
x3
= 0 → Mx3 = 0
x3
= 2 m → Mx3 = -60 kNm (∩)
Lx3
= 30 kN (↿⇂)
Nx3
= 30 kN (tarik)
Interval 4 (0 < x4
< 5m)
Mx4
= - 30 (2 + x4) - q x4
(0.5 x4) + VB (x4)
= -20 x42 +
171.25 x4 - 60
x4
= 0 → Mx4 = 0
x4
= 2.5 m → Mx4 = 243.125 kNm (∪)
x4
= 5 m → Mx4 = 296.25 kNm (∪)
Mencari
letak dan besaran momen maksimum : Lx
= 0
-40
x4 + 171.25 = 0 → x4 = 4.28125 m
Mmax
= -20 (4.28125) 2 + 171.25 (4.28125)
- 60= 306.5820 kNm
Lx4
= 30 - VB + q x4
= 171.25 + 40x4
x4
= 0 → Lx4 = -171.25 kN (⇃↾)
x4
= 5 m → Lx4 = 28.75 kN (↿⇂)
Nx4
= 30 kN (tarik)
Gambar Bidang Gaya Dalam (M, L, N) *tidak berskala
Bidang Momen Lentur
Bidang Gaya Lintang
Bidang Gaya Normal
Soal 3: Balok Kantilever
Hitung dan gambar bidang M, L, N
Σ V = 0 → VA - (40 x 3) - 60 = 0
VA = 180 kN (↑)
Σ H = 0 → -HA + 60 = 0
HA = 60 kN (←)
Σ MA = 0 → -MA + 120(1.5) + 60(6)
= 0
MA = 540 kN m (↺)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Interval 1 (0 < x1
< 3m)
Mx1 =
-MA + VA x1 - q x1 (0.5 x1)
=
-20 x12 + 180 x1 - 540
x1 = 0 → Mx1 = -540 kN m (∩)
x1 = 1.5 m → Mx1 = -315 kN m (∩)
x1 = 3 m → Mx1 = -180 kN m (∩)
Lx1 = VA - 40x1 = 180
- 40x1
x1 = 0 → Lx1 = 180 kN (↿⇂)
x1 = 3 m → Lx1 = 60 kN (↿⇂)
Nx1 = HA = 60 kN (tarik)
Interval 2 (0 < x2
< 3m)
Mx2 = -60x2
x2 = 0 → Mx2 = 0
x2 = 3 m → Mx2 = -180 kN m (∩)
Lx2 = 80 kN (↿⇂)
Nx2 = 60 kN (tarik)
Gambar Bidang Gaya Dalam (M, L, N) *tidak berskala
Soal 4: Portal Jepit Bebas
Hitung dan gambar bidang gaya dalam
tan
α = 1.5 / 3 = 0.5
α
= 26.5651°
tan
β = 1.5 / 4 = 0.275
β
= 20.5560°
Σ
V = 0 → VA - 160 - 20 = 0
VA
= 180 kN (↑)
Σ
H = 0 → -30 + HA = 0
HA
= 30 kN (→)
Σ
MA = 0 → 160 (2) - 30(6 + 1.5) - 20(3) - MA = 0
MA
= 35 kN m (↺)
Interval
untuk gaya dalam ditentukan sebagai berikut :
Interval 1 (0 < x1
< 6 m)
Mx1
= -MA - HA x1 = -35 - 30x1
x1
= 0 → Mx1 = -35 kNm (∩)
x1
= 6 m → Mx1 =-215 kNm (∩)
Lx1
= -HA = -30 kN (⇃↾)
Nx1
= -VA = -180 kN (tekan)
Interval 2 (0 < x2
< 3 m)
Mx2
= -20x2
x2
= 0 → Mx2 = 0
x2
= 3 m → Mx2 = -60 kNm (∩)
Lx2
= -P cos α = -20 cos (26.5651° ) = -17.8892 kN
(⇃↾)
Nx2
= -P sin α = -20 sin (26.5651°) = - 8.9443 kN (tekan)
Interval 3 (0 < x3
< 4 m)
Mx3
= -q x3 (0.5 x3)
+ 30 tan β x3
= -20x32 +
11.25 x3
x3
= 0 → Mx3 = 0
x3
= 2 m → Mx3 = -57.5 kN m
x3
= 4 m → Mx3 = -275 kN m
Letak
dan besar momen maksimum :
x3 = 0.2812 m
Mmax = -20(0.2812) 2 + 11.25
(0.2812) = 1.582 kN m (∪)
Lx3 =
q x3 cos β - 30 sin β
=
37.4532 x3 - 10.5337
x3 = 0 → Lx3 = -10.5337 kN (⇃↾)
x3 = 4 m → Lx3 = 139.2591 kN (↿⇂)
Nx3 =
-q x3 sin β - 30 cos β
=
-14.0449 x3 - 28.0899
x3 = 0 → Nx3 = -28.0899kN (tekan)
x3 = 4 m → Nx3 = -84.2695 kN (tekan)
Check keseimbangan momen titik B
Σ MB = 0 → 215 +60 - 275 = 0 (OK)
Bidang Momen Lentur
Bidang Gaya Lintang
Bidang Gaya Normal
Soal 5 : Portal dengan beban lateral / horisontal
Hitung
dan gambar bidang M, L, N
Pada
soal ini, arah reaksi perletakan diasumsi sebagai berikut :
VA
ke atas (↑)
VB
ke atas (↑)
HB
ke kanan (→)
tan
α = 4/3 sin α = 0.8 cos α = 0.6
Σ
H = 0 → HB - 1200 + (800 x 4) = -2000 kg (asumsi salah)
HB
= 2000 kg (←)
Σ MA = 0 → (800 x 4) (2) - 1200 (4) - VB
(4) = 0
4 VB = 1600
VB = 400 kg (↑)
Σ MB = 0 → (800 x 4) (2) - 1200 (4) + VA
(4) = 0
4 VA
= -1600
VA = -400 (pemisalan salah)
VA = 400 kg (↓)
Interval untuk menghitung gaya dalam ditentukan sebagai
berikut :
Interval
1 (0 < x1 < 4m)
Mx1
= -0.5 q x12 = -40 x12
x1
= 0 → Mx1 = 0
x1
= 2 m → Mx1 = -1600 kg m (∩)
x1
= 4 m → Mx1 = -6400 kg m (∩)
Lx1
= -q x1 = -800 x1
x1
= 0 → Lx1 = 0
x1
= 4m → Lx1 = - 3200 kg (⇃↾)
Nx1
= VA = 400 kg (tarik)
Interval
2 (0 < x2 < 7 m)
Mx2
= -VA x2 - (800 x 4)2 = -400 x2 - 6400
x2
= 0 → Mx2 = -6400 kg m
x2
= 7 m → Mx2 = -9200 kg m
Lx2
= -VA = - 400 kg (⇃↾)
Nx2
= - (800 x 4) = -3200 kg (tekan)
Interval
3 (0 < x3 < 3 m)
Mx3
= -VB x3 - HB (4/3 x3) = -3066.667
x3
x3
= 0 → Mx3 = 0
x3
= 3 m → Mx3 = -9200 kg m
Lx3
= VB cos α + HB sin α
= 400 (0.6) + 2000 (0.8) = 1840 kg (↿⇂)
Nx3
= -VB sin α + HB cos α = -400 (0.8) + 2000 (0.6) = 880 kg
(tarik)
Bidang
Gaya Dalam (*tidak berskala)
Bidang Momen Lentur
Bidang Gaya Lintang
Bidang Gaya Normal




















No comments:
Post a Comment