Penguraian dan Penjumlahan Vektor Gaya

Penguraian Gaya dan Gaya Resultan

Gaya merupakan vektor, sehingga mempunyai besar dan arah.  Karena beberapa gaya dapat bekerja pada suatu sistem dengan berbagai arah, gaya harus diuraikan menjadi komponen X dan komponen Y agar perhitungannya lebih muda.

Sebelum memulai penguraian gaya, dalil Pitagoras dan perbandingan trigonometri (sin, cos, tan) harus dikuasai.

Dalil Pitagoras (Pythagorean Theorem) 

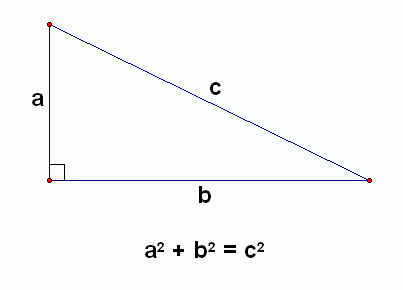Pada satu segitiga tegak, terdapat dua sisi yang lurus/tegak dan satu sisi yang miring.  Dengan menggunakan rumus pitagoras, kita dapat mencari besaran/panjang sisi miring tersebut dengan hanya mengetahui besaran/panjang kedua sisi yang lain. Hal ini juga berlaku untuk suatu gaya. Contoh diketahui satu gaya yang sejajar sumbu X dengan besaran tertentu dan satu gaya yang sejajar sumbu Y dengan besaran tertentu dan kedua gaya tersebut memiliki titik kerja/pegang yang sama.  Dari informasi ini, kita dapat mencari satu gaya dengan besaran dan arah yang sama dengan jumlah/gambungan kedua gaya awal dan bekerja pada titik pegang yang sama juga.

Perbandingan Trigonometri:
Perbandingan trigonometri terdapat tiga fungsi dasar yaitui, Sin, Cos, dan Tan.  Ketiga fungsi ini akan sangat membantu dalam menentukan arah gaya resultan dan penguraian gaya miring.
Pertama misalkan terdapat dengan kaki x, kaki y, sisi miring h, dan sudut teta.  Di sini, kaki x adalah sisi yang ada di samping sudut teta, kaki y adalah sisi yang ada di depan sudut teta.  Maka akan diperoleh perbandingan seperti berikut

                  atau

Maka akan diperoleh:

Sisi Depan Sudut = Sisi Miring × Sin(Ѳ)

Sisi Samping Sudut = Sisi Miring × Cos(Ѳ)

Fungsi Invers Trigonometri juga dipakai untuk mencari besar sudut bila dua sisi sudah diketahui.

θ = arcsin (depan / miring)

θ = arccos (samping / miring)

θ = arctan (depan / samping)

*pada kalkulator, fungsi invers trigonometri ditandai dgn :

arcsin = sin^-1 

arccos = cos^-1

arctan = tan^-1

Contoh-contoh soal:

1.  diketahui θ = 60º
c = 10

Hitunglah a dan b

cos θ = a/c
a = c * cos θ
   = 10 * cos 60
a = 5

sin θ = b/c
b = c * sin θ
   = 10 * sin 60
b = 8,66

Jawaban dapat dicek menggunakan rumus pitagoras.

a² + b² = c² 

5² + 8,66² = 10²

25 + 75 = 100

100 = 100 (ok)

2.  Bila diketahui
a = 6
b = 10

Hitunglah c dan sudut θ

a² + b² = c²

6² + 10² = c² 

36 + 100 = c²

136 = c² 

c = 11,66

θ = arctan (depan / samping)

θ = arctan (b / a)

θ = arctan (10 / 6)

θ = 59,04º

3. Terdapat gaya miring P = 45 kN seperti digambar yang bekerja dengan sudut 53 derajat.

Hitung komponen X (horisontal) dan Y (vertikal) gaya tersebut.

Px = P cos θ
     = 45kN * cos 53
     = 27,08 kN

Py = P * sin θ
     = 45kN * sin 53
     = 35,94 kN





Cara graifs.
Suatu vektor dapat diurai atau dijumlahkan dengar cara menggambar gaya tersebut.
Untuk penguraian suatu vektor menjadi komponen X(horisontal) dan Y(vertikal) :

1. Tentukan skala. Contoh 10kN = 1 cm
2. Gambar gaya sesuai skala (panjang) dan arah (sudut) yang benar.
3. Tarik garis horisontal dan vertikal di ujung anak panah.
4. Tarik garis horisontal & vertikal mulai di titik kerja sampai garis dari langkah no 3
5. Ukur garis tersebut sesuai skala yang ditentukan untuk mendapat besaran gaya
6. Anggaplah titik kerja sama dengan gaya semula.

Untuk penjumlahan atau mencari gaya resultan:

1. Gambar gaya pertama sesuai skala dan arah.
2. Gambar gaya berikutnya mulai di ujung anak panah gaya sebelumnya (titik kerja gaya baru ada di anak panah gaya sebelumnya)
3. Menysusun semua gaya dengan langkah no 2.
4. Tarik garis dari titik kerja gaya pertama ke ujung anak panah gaya terakhir.  Itu adalah gaya resultan.
5. Ukur garis tersebut sesuai skala yang ditentukan untuk mendapat besaran gaya
6. Ukur sudut (pakai busur) dari garis horisontal untuk mendapat arah.